Tablouri de elemente

Tablouri de elemente

La fel ca in celelalte medii de programare, tablourile sunt extrem de utile si in consecinta sunt des utilizate.
LabVIEW ofera o metoda rapida pentru crearea si initializarea tablourilor.

Crearea si initializarea tablourilor de elemente

Vom crea si vom initializa pentru inceput un vector cu 8 elemente binare. Vom crea un VI vector_v0 pe care vom plasa un control de tip Array. Controlul de tip Array se gaseste in : Controls => Modern => Array, Matris & Cluster (Data Containers) => Array. Tinand cont ca vrem sa initializam un vector cu elemente binare, vom plasa pe panoul frontal un control boolean de tip LED. In acest moment panoul frontal arata astfel:

Vom selecta ledul si il vom "trage" cu mouse-ul peste controlul array creat anterior. In acest moment panoul frontal arata astfel:

Redimensionam vectorul creat pana apar 8 LED-uri si schimbam proprietatea Label cu "Vector LED-uri". In acest moment panoul frontal arata astfel:

In acest moment, alegand din Tools->Operate Value, putem sa schimbam starea ledurilor si sa atribuim dupa dorinta diverse valori (0 sau 1) LED-urilor. Avem in acest moment:

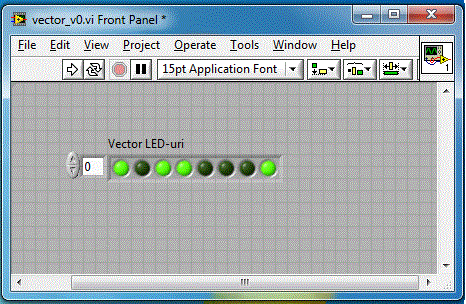
Am creat si am initializat astfel un vector cu 8 elemente de tip boolean.

Citirea valorii unui element al tabloului

Odata creat si initializat un tablou de elemente, elementele acestuia pot fi selectate pentru a citi valoarea elementului respectiv.
Sa presupunem ca am creat un vector de elemente, pe care le-am initializat. Urmatoarea aplicatie citeste elementul dorit din vector. Vom crea deci un VI vector_v1 de forma:

Avem nevoie de o functie care sa selecteze un anumit element de la un anumit index. Functia se numeste Index Array si se gaseste in grupul Functions => Programming => Array => Index Array. Diagrama bloc arata astfel:

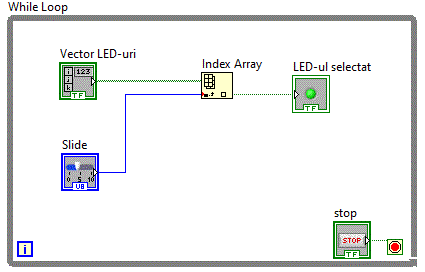
Se observa ca Index Array are nevoie de tabloul si indexul in cadrul tabloului si furnizeaza valoarea elementului.

Scrierea valorii unui element al tabloului

Operatia inversa citirii valorii unui element, este operatia de scriere a valorii unui element. In cazul unui vector binar, operatia mai poate fi numita si setarea valorii unui element.
Urmatoarea aplicatie scrie valoarea unui element al unui vector. Vom crea deci un VI vector_wr de forma:

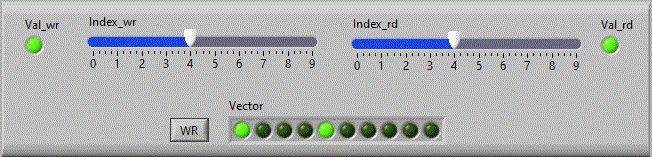
Avem nevoie de o functie care sa selecteze un anumit element de la un anumit index si sa inlocuiasca valoarea existenta cu valoarea dorita. Nu exista o astfel de functie, insa putem folosi functia "Replace Array Subset" care se gaseste in grupul Functions => Programming => Array => Replace Array Subset. Pentru a putea folosi aceasta functie pentru scrierea valorii unui element vom atribui vectorul "Vector" atat intrarii "array" si pentru "output array". Acest lucru este posibil numai daca definim variabila locala "Vector". Diagrama bloc va arata astfel:

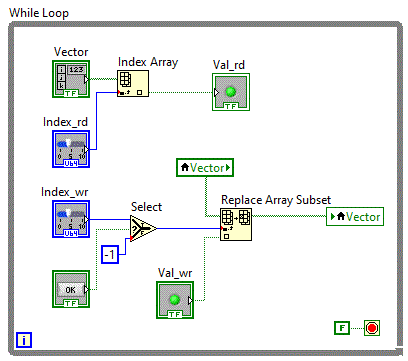
    Pentru a controla momentul in care se va inscrie valoarea, a fost nevoie sa mai adaugam un buton "WR" care valideaza valoarea index-ului numai la apasarea butonului. Daca butonul "WR" nu este apasat, valoarea index-ului fiind -1, valoare care nu selecteaza nici un element al vectorului, index-ul pornind de la valoarea 0.
    Setarea valorilor elementelor unui tablou poate fi facuta si prin atribuirea directa de valori pentru fiecare element.
    In urmatoarea aplicatie vector_v2 se vor genera numere aleatoare intre 0 si 256 , fiecare numar va fi convertit in 8 biti care vor fi atribuiti unui vector boolean cu dimensiunea 8. Numerele vor fi generate la un interval de 100 ms deci afisand continutul vectorului vom obtine aprinderea aleatoare a bitilor ce compun vectorul.

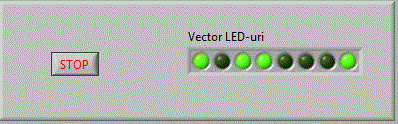
Diagrama logica va contine un convertor Number to Boolean Array

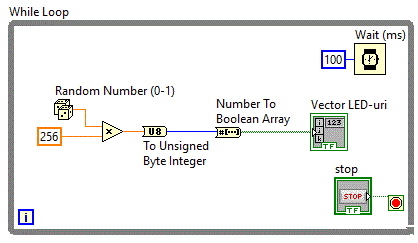
Valoarea numerica aleatoare intre 0 si 256 va fi convertita intr-un vector boolean pe 8 biti care este atribuit vectorului cu LED-uri care va fi afisat pe panoul frontal.

Vectori de elemente

Am creat in aplicatiile anterioare tablouri unidimensionale de elemente. Tablourile unidimensionale mai poarta denumirea de vectori. In aplicatiile anterioare am creat si am initializat vectori booleeni. Vectorii pot contine orice fel de elemente. Dupa principiul dupa care am creat vectorii booleeni, vom crea acum vectori care vor contine elemente de tip numeric.
Vom crea acum o aplicatie vector_v3 unde vom plasa un control de tip vector cu 10 elemente numerice double. Acest control va permite modificarea fiecarui element din vector precum si selectarea si afisarea separata a unui element selectat prin intermediul unui control numeric ce reprezinta indexul in vector.

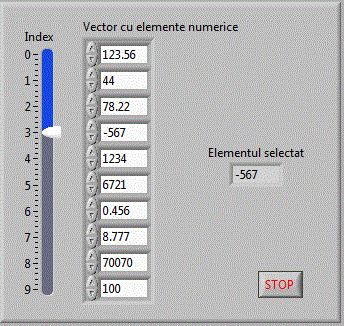
Diagrama bloc a aplicatiei foloseste functia "Index Array" pentru a selecta elementul dorit.

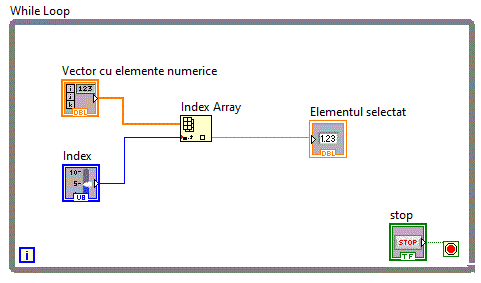
Elementele vectorului pot fi inscrise si prin alte metode, cum ar fi atribuirea cate unui numar fiecarui element.
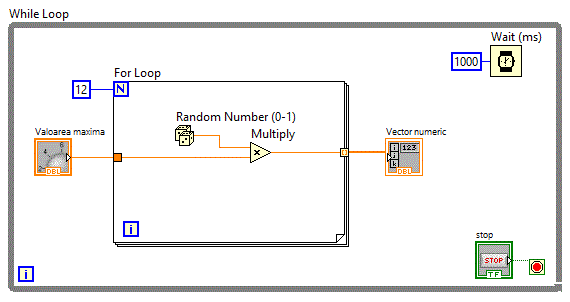
Urmatoarea aplicatie vector_v4 atribuie cate un numar aleator fiecarui element al vectorului.

Atribuirea cate unui numar aleator fiecarui element al vectorului este o procedura repetitiva. Vom folosi deci structura de programare repetitiva For Loop.

Se observa ca iesirea din structura de programare repetitiva For Loop are " dimensiunea tablou de elemente" fiind reprezentata cu o linie mai groasa.

Matrici de elemente

Bazandu-ne pe aplicatiile cu vectori booleani, vom realiza acum o matrice booleana. Urmatoarea aplicatie matrici_v0 utilizeaza o matrice booleana de 16X16.

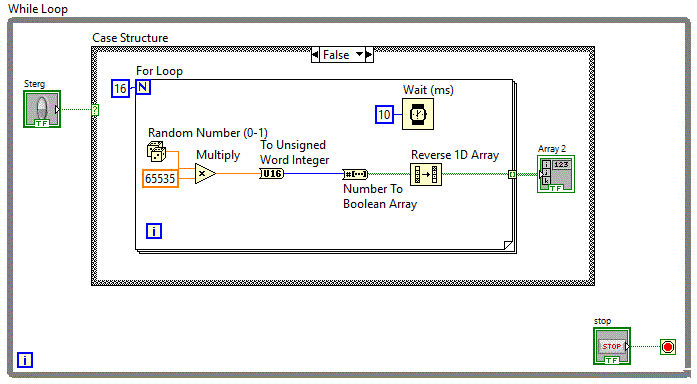
Diagrama bloc va fi asemanatoare cu diagrama aplicatiei vector_v2 cu diferenta ca va trebui reluata pentru mai multe linii.

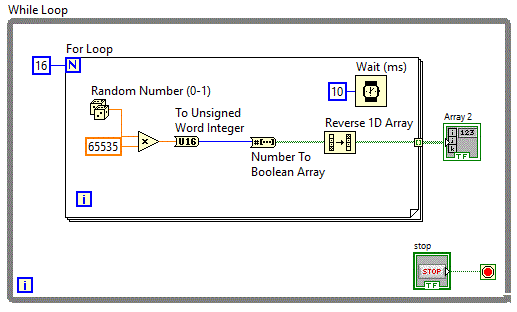
    Diagrama bloc contine deci o structura repetitiva for care repeta de 16 ori inscrierea a cate 16 biti
    Sa imbunatatim aplicatia anterioara si sa adaugam un buton care sa initializeze cu o matricea cu alte cuvinte sa stinga toate LED-urile. Obtinem astfel aplicatia: matrici_v1
    Vom plasa un buton caruia i se seteaza operatia "Switch until Released". Dupa apasare matricea de LED-uri se va sterge si va ramane stearsa pentru 500 ms. Pentru a se realiza aceasta functionalitate se va folosi o structura decizionala "Case Structure". Pe perioada cand este actionat butonul, aplicatia trebuie initializeze matricea cu 0 si sa astepte 500 ms

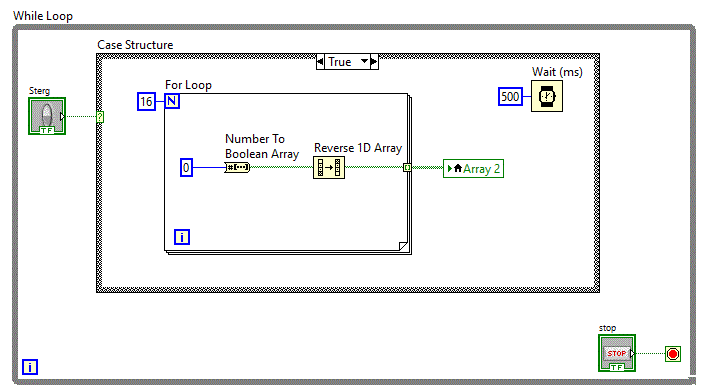
Pe perioada cand nu este actionat butonul, aplicatia trebuie sa execute diagrama bloc din aplicatia anterioara.

Matrici de LED-uri 7X5

Matricile de LED-uri de dimensiune 7X5, sunt realizate fizic fiind produse de diverse firme de componente electronice.

Sa utilizam acum o matrice de LED-uri de dimensiune 7X5. Sa incercam sa formam din LED-uri aprinse cifrele de la 1 la 9. Pentru fiecare caracter pe care urmam sa-l afisam, va trebui sa definim cate o matrice 7X5 in care sunt setate in mod corespunzator valorile pentru fiecare element.Astfel pentru caracterul "2" va trebui sa definim o matrice cu elementele setate astfel:

In aplicatia matrici_v2 , definim 10 matrici binare in care vom seta elementele care corespund LED-urilor aprinse in cadrul unei cifre.

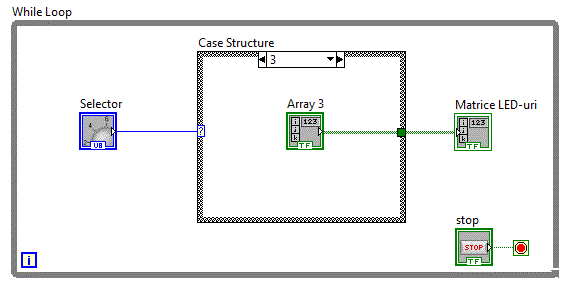
Vom folosi o structura decizionala "Case Structure" cu 10 optiuni si vom plasa in cadrul fiecarei optiuni matricea corespunzatoare. Astfel de exemplu pe optiunea 3 punem:

Selectarea elementelor apartinand unei matrici

Avand o matrice de diverse elemente, se pune problema cum accesam aceste elemente. La fel cum am selectat un element apartinand unui vector, putem accesa un element, o linie sau o coloana apartinand unei matrici. Functia care ne permite aceasta operatie este aceeasi functie utilizata pentru vectori si anume: Index Array plasata in grupul Functions => Programming => Array => Index Array.

Sa realizam o aplicatie matrici_v3 in care avanad o matrice de elemente binare vom selecta o anumita linie si o vom afisa utilizand un control sub forma de vector de LED-uri.

Diagrama bloc va contine functia Index Array

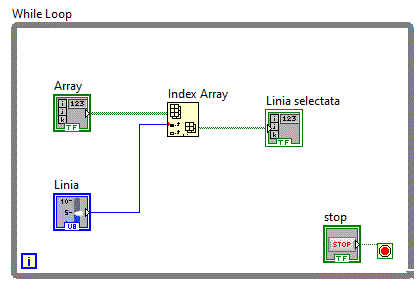
Dupa cum se observa, functiei Index Array i s-a furnizat un singur parametru respectiv numarul liniei.

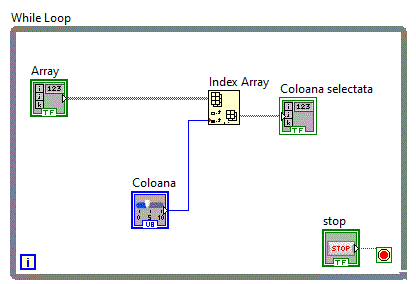
dupa acelasi principiu, sa realizam o aplicatie matrici_v4 in care avanad o matrice de elemente binare vom selecta o anumita coloana si o vom afisa utilizand un control sub forma de vector de LED-uri.

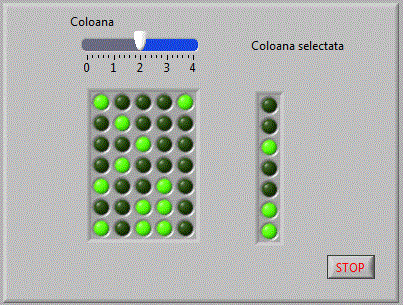
In diagrama bloc,vom furniza functiei Index Array, un singur parametru si anume numarul coloanei.

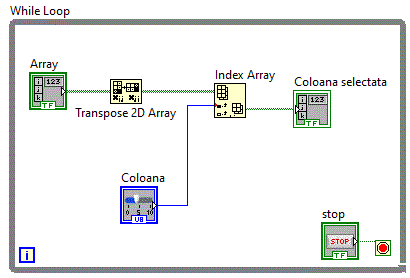
Am putea selecta o coloana furnizand functiei Index Array in loc de parametrul numarul coloanei, numarul liniei matrici_v5 , cu conditia sa transpunem maricea utilizand functia Transpose 1D Array, ceva asemanator cu diagrama bloc de jos:

Combinand selectia unei linii cu selectia unei coloane, obtinem aplicatia: matrici_v6

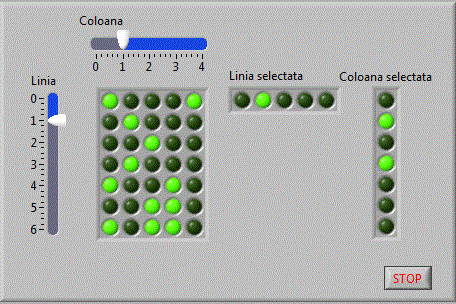
Diagrama bloc fiind:

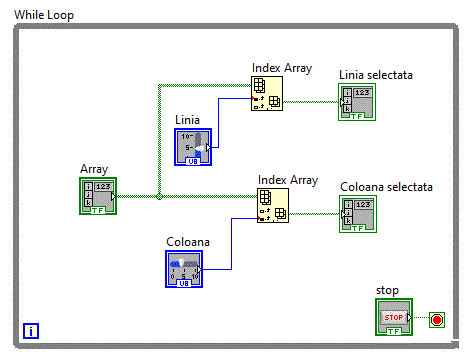
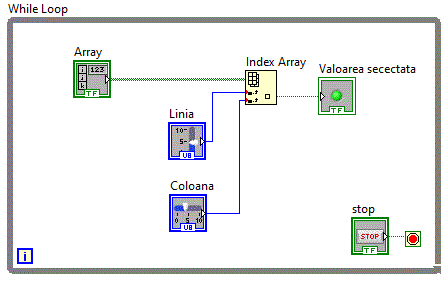
Pentru selectia unui singur element matrici_v7

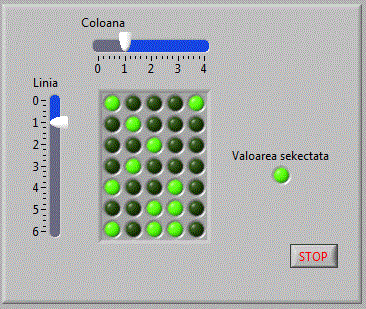
Vom furniza functiei Index Array simultan cei doi parametrii, respectiv numarul liniei si numarul coloanei.

Matrici numerice

Tablourile pot contine orice fel de elemente. Vom utiliza in continuare o matrice numerica in care elementele numerice vor fi inscrise cu numere aleatoare matrici_v8 .

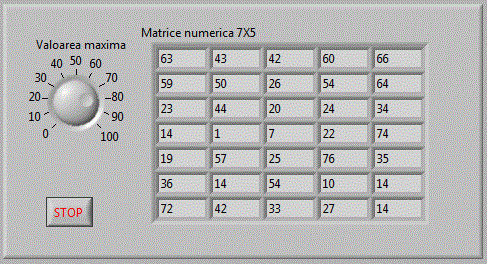
Pentru a inscrie toate elementele matricii 7X5 vom avea nevoie de o dubla iteratie.

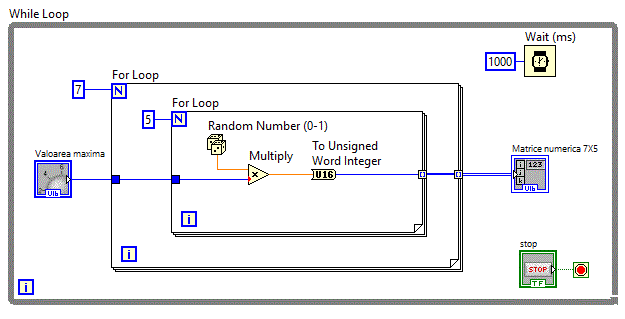
Selectia elementelor se face similar folosind functia Index Array. Vom completa aplicatia anterioara cu selectia unui anumit element matrici_v9 .

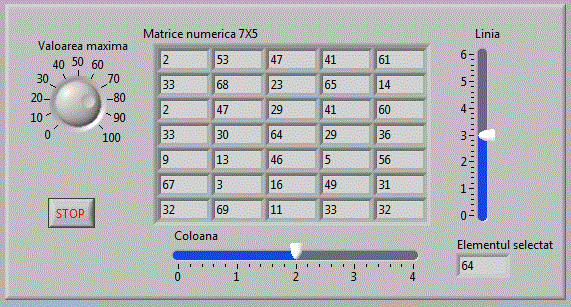
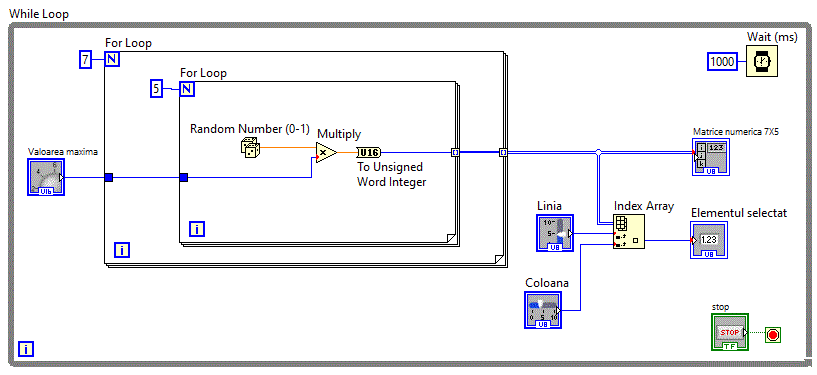
Diagrama bloc fiind:

Matrici cu numere reale

    Dupa cum am amintit matricile sunt tablouri bidimensionale. Putem oricand crea matrici prin plasarea unui tablou caruia ii setam dimensiunea la 2. Avand in vedere importanta matricilor care contin numere reale sau imaginare, s-au creat cotroale speciale pentru matricile cu numere reale si matricile cu numere imaginare. Aceste controale sunt plasate in: Controls => Modern => Array, Matris & Cluster => RealMatrix respectiv in Controls => Modern => Array, Matris & Cluster => ComplexMatrix.

    Sa realizam acum o aplicatie care utilizeaza matrici reale matrici_v30 .
    In cadrul acestei aplicatii se va realiza o matrice reala de dimensiune 7X5 in care or fi inscrise numere aleatoare dupa fiecare 400 ms.

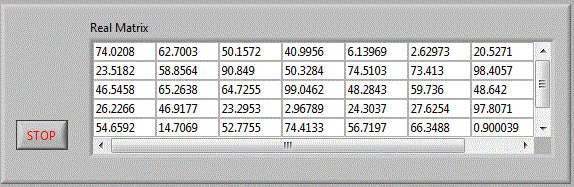
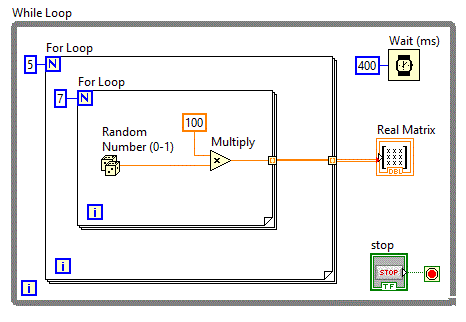
Diagrama bloc va contine o dubla cilare pentru a inscrie elementele matricii.

Matrici cu numere imaginare

Dupa o metoda similara cu metoda de sus se pot crea si utiliza matrici cu numere imaginare. Vom crea in continuare o aplicatie matrici_v31 , in care va realiza o matrice imaginara de dimensiune 3X5 in care vor fi inscrise numere aleatoare dupa fiecare 400 ms.

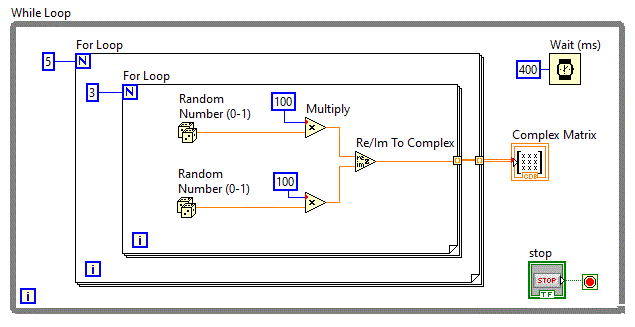
In diagrama bloc va fi utilizata functia "Re/Im To Complex" functie aflata in: Function => Programming => Numeric => Complex => Re/Im To Complex

Tablouri 3D

Se pot defini tablouri cu oricate dimensiuni. Ne vom opri totusi la tablouri cu 3 dimensiuni. Folosind matrici de LED-uri putem defini practic aproape orice simbol (litera sau cifra). Ne propunem sa afisam caracterele de la 0-9 folosind matrici de LED-uri. Va trebui sa definim deci 10 matrici boolene care sa contina cele 10 simboluri. Practic definim un singur tablou 3D cu dimensiunea 7X5X10. Din tablul 3D se pot face diverse selectii cum ar fi : o matrice, o coloana, un rand, un element. Selectand o matrice, vom selecta practic simbolul unui anumit caracter. matrici_v20

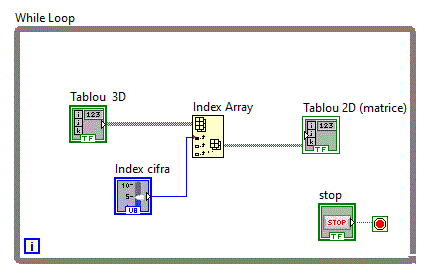
Elementele tabloului 3D trebuiesc setate corespunzator cu simbolurile cifrelor dupa care selectand o anumita matrice folosind functia Index Array, si afisand-o intr-o matrice de leduri, se afiseaza cifra dorita.

Utilizarea tablourilor pentru afisarea grafica

Majoritatea controalelor grafice presupun utilizarea tablourilor. In general afisarea datelor in mod grafic se face prin intermediul tablourilor, tablouri care pastreaza datele ce urmeaza a fi reprezentate grafic.
Astfel pentru afisa grafic valorile unui vector, se foloseste controlul Waveform Graph aflat in grupul : Controls => Modern => Graph => Waveform Graph vector_v5 .

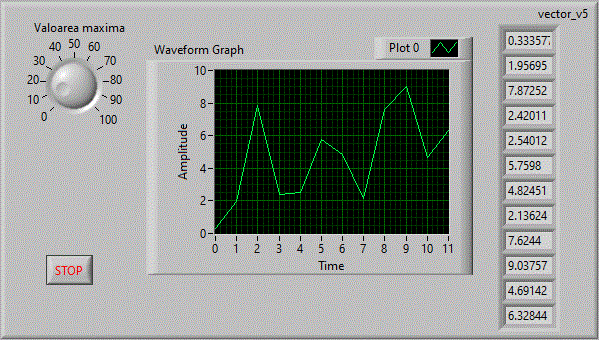
Diagrama bloc va contine deci si o legatura spre controlul grafic Waveform Graph.

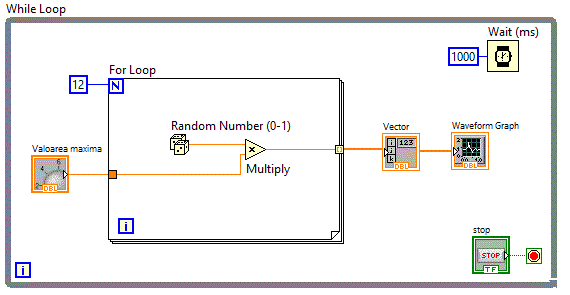
    Dupa cum se observa, ontrolul grafic Waveform Graph, admite la intrare un Array 1D pentru afisare Single Plot.
    Functiile de tipul z=f(x,y) pot fi reprezentate grafic sub forma de suprafete. Reprezentarea suprafetelor 3D implica utilizarea a doi vectori care pastreaza valorile pentru x respectiv y si un tablou bidimensional in care vor fi pastrate valorile functiei f(x,y). Pentru a reprezenta acest tip de functii, exista controale grafice specilae. In aplicatia urmatoare matrici_v40 vom folosi controlul 3D aflat in grupul: Control => Modern => Graph => 3D Graph => Surface. 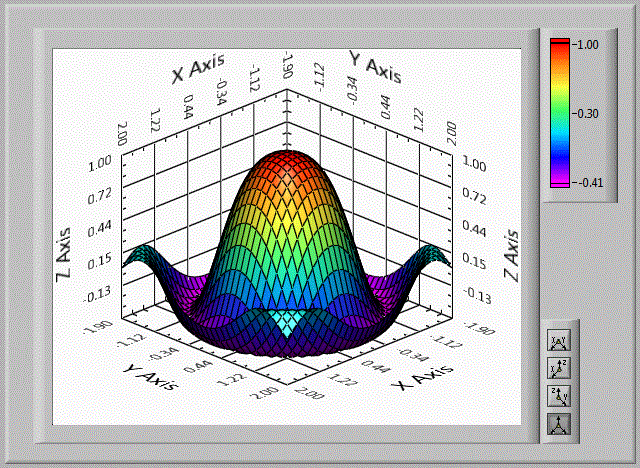pentru a reprezenta grafic functia:
z=cos(x²+y²)e^{-0.3(x²+y²)}
    Transpusa in limbaj C++ functia devine:
z=cos(x*x+y*y)*exp(-0.3*(x*x+y*y));

In diagrama bloc se va folosi o structura "Formula node" pentru a introduce expresia functiei.

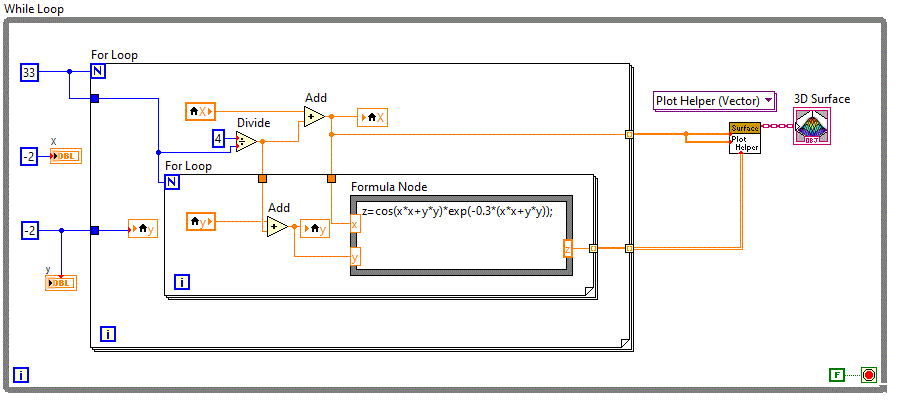Dupa cum se observa, controlul 3D Graph => Surface are nevoie de trei tablouri pentru a afisa graficul functiei.

Pentru a modifica rezolutia cu care se afiseaza suprafata, mai adaugam un control numeric. matrici_v41

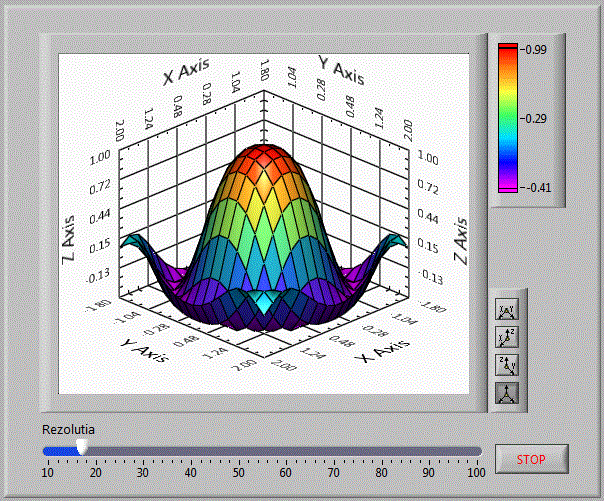
Diagrama bloc fiind:

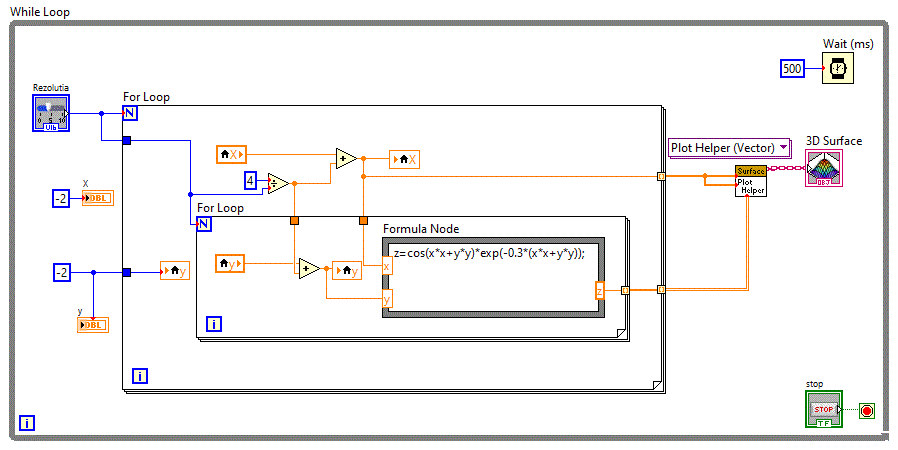
Pentru a modifica domeniul de definitie al functiei, adaugam un control numeric astfel: matrici_v42

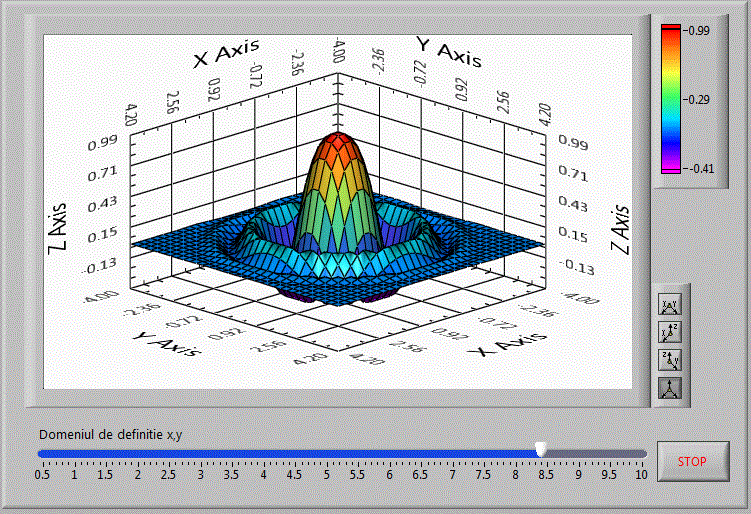
Diagrama bloc fiind:

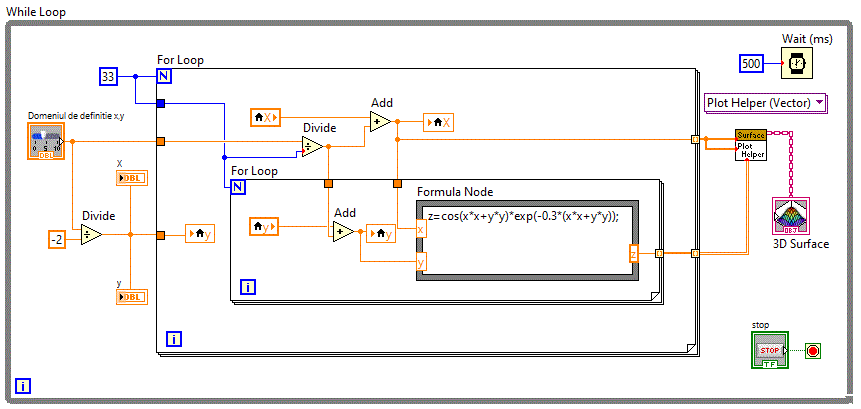
De multe ori e necesara vizualizarea unei curbe in spatiu. Astfel am putea reprezenta grafic traseul uniui avion care se deplaseaza in trei coordonate. Pentru inceput vom reprezenta functia sin(x) iar y va fi o constanta (in cazul nostru y=1) matrici_v43
Pentru afisare vom folosi controlul 3D Graph plasat in grulpul: Controls => Modern => Graph => 3D Graph => Line Graph

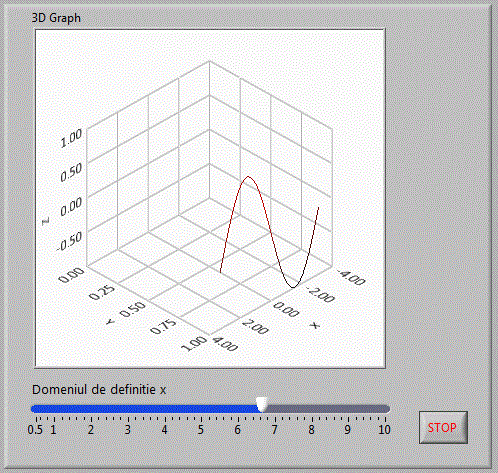
Diagrama bloc fiind:

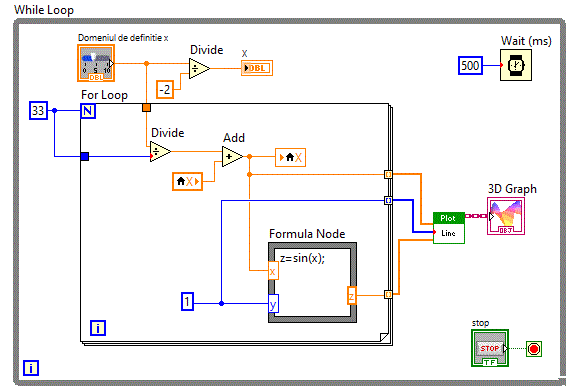
Vom folosi acelasi control dar vom afisa de data aceasta functia reprezentata anterior sub forma de suprafata z=cos(x²+y²)e^{-0.3(x²+y²)} dar de data aceasta sub forma de linie 3D. matrici_v44

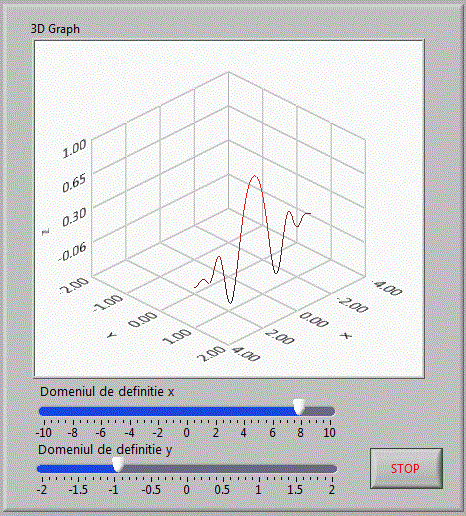
Diagrama bloc fiind:

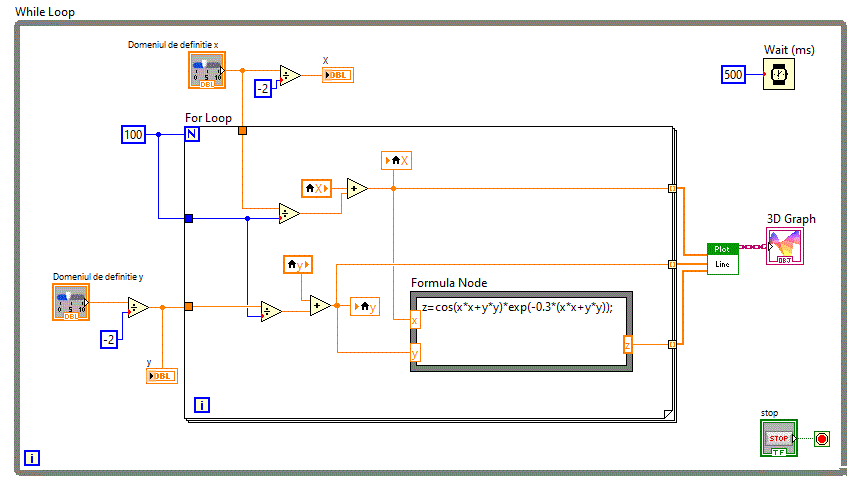
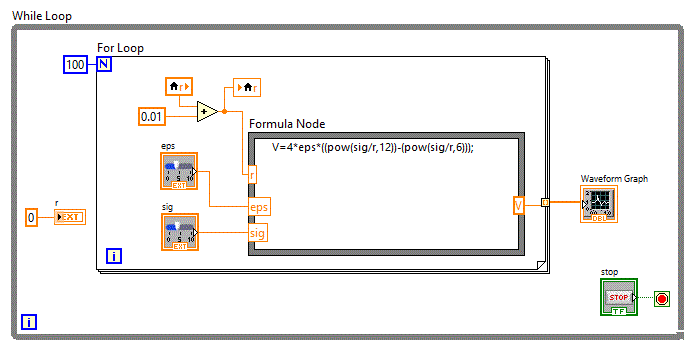
Vom folosi in continuare in aplicatia matrici_v50 controale grafice si vom afisa functia de potential a lui Lennard Jones
V=4eps[(sig/r)¹²-(sig/r)⁶]
Transpusa in limbaj C++ functia devine:
V=4*eps*((pow(sig/r,12))-(pow(sig/r,6)));

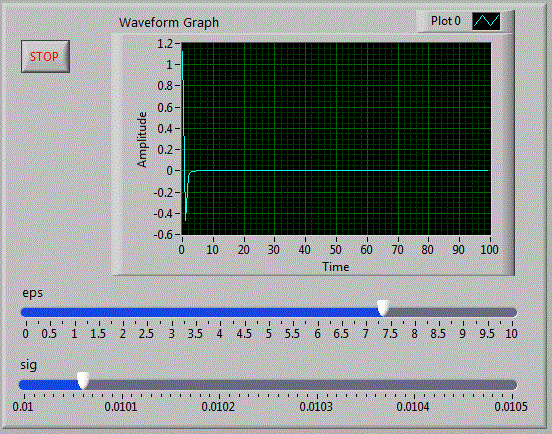
Diagrama bloc fiind:

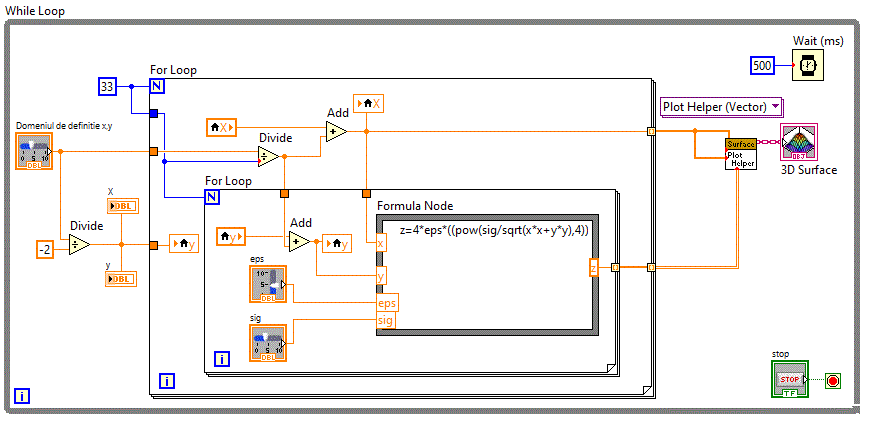
In aplicatia matrici_v51 , vom reprezenta in spatiu potentialul in jurul unei moecule folosind un control grafic 3D , plecand de la functia de potential Lennard Jones realizand o functie de doua variabile x si y egale intre ele
z=4eps{[(sig/√(x²+y²)]⁴ - [sig/√(x²+y²)]²}
Transpusa in limbaj C++ functia devine:
z=4*eps*((pow(sig/sqrt(x*x+y*y),4))-(pow(sig/sqrt(x*x+y*y),2)));

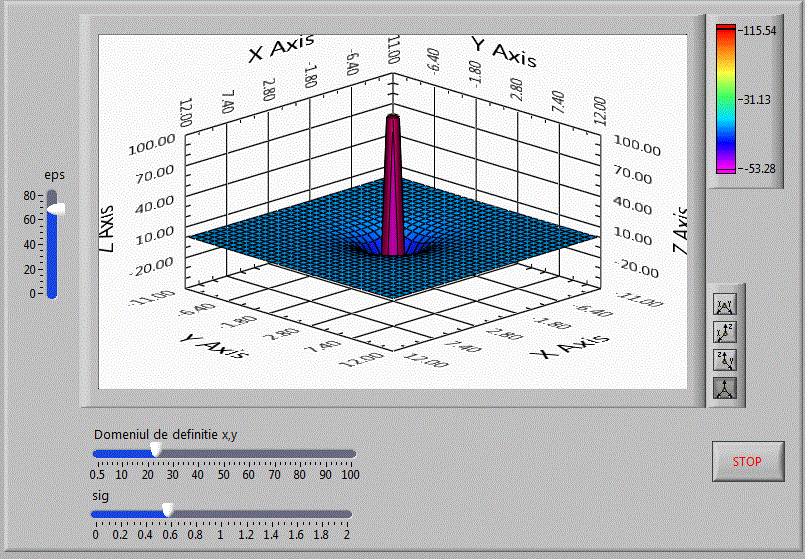
Diagrama bloc fiind: