// Program scris in C++ Visual Studio 2005 de tipul:CLR console application
// Expresii relationale
#include "stdafx.h"
#include < iostream >
using namespace std;
int main()
{
double a,b;
cout << "\n\tIntroduceti o valoare pentru numarul a : ";
cin >> a ;
cin.ignore();
cout << "\n\tIntroduceti o valoare pentru numarul b : ";
cin >> b;
cin.ignore();
cout <<"\n\n\tOperatia : a > b are ca rzultat: " << (a>b);
cout <<"\n\tOperatia : a >= b are ca rezultat: " << (a>=b);
cout <<"\n\tOperatia : a == b are ca rezultat: " << (a==b);
cout <<"\n\tOperatia : a != b are ca rezultat: " << (a!=b);
cout <<"\n\tOperatia : a <= b are ca rezultat: " << (a<=b);
cout <<"\n\tOperatia : a < b are ca rezultat: " << (a < b);
cin.get();
return 0;
}
|
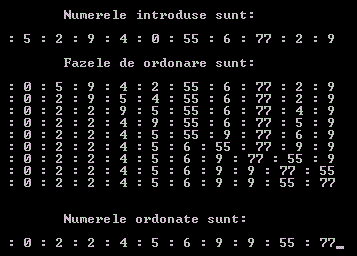
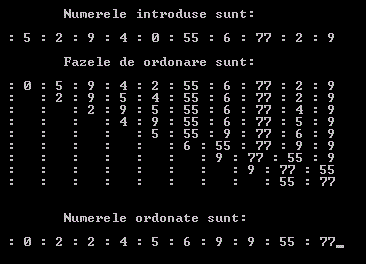
Dupa rularea programului in "Command Prompt" se afiseaza:
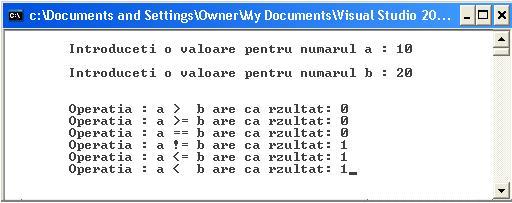
Schemele logice – au rolul de a reprezenta grafic fluxul general al datelor si a algoritmului de prelucrare.
Sintetizeaza succesiunea etapelor de rezolvare a unei probleme constituind o reprezentare grafica a functiilor algoritmului utlizat. In cadrul acestor scheme se folosesc simboluri standard, carora li se asociaza în principiu anumite instructiuni.
Schema logica reprezinta de fapt un graf orientat în care exista cel putin urmatoarele elemente:
- o instructiune de pornire (START) si una de oprire (STOP);
- instructiuni de atribuire;
- instructiuni de citire a datelor;
- instructiuni de decizie;
- instructiuni de scriere/afisare a rezultatelor prelucrarii.
- sageti care indica sensul fluxului de prelucrare, deci ordinea de executie a operatiilor elementare.
Ordinea în care instructiunile programului sunt executate constituie structura de control a acestuia.
Schema logica este importanta la analiza problemei, la scrierea programuli si la intelegerea programului de alte persoane, schema logica fiind reprezentarea vizuala a functionarii programului.
Se folosesc urmatoarele simboluri grafice in cadrul schemelor logice

Schema logica a programului care asteapata de la utilizator raza unui cerc si afiseaza aria acestuia , arata astfel:
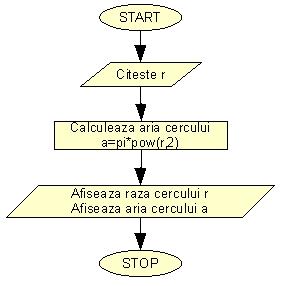
Sunt cazuri in care programul trebuie sa ruleze anumite instructiuni numai in anumite cazuri. Sa presupunem ca un program asteapta doua numere de la utilizator si vrea sa calculeze diferenta lor si s-o afiseze insa inainte sa afiseze diferenta numerelor introduse am vrea sa fim avertizati cu un mesaj ca diferenta este negativa. Deci instructiunea care afiseaza mesajul "Diferenta este negativa", trebuie sa se execute numai daca diferenta dintre numerele introduse este negativa. Schema logica a unui astfel de program arata astfel:
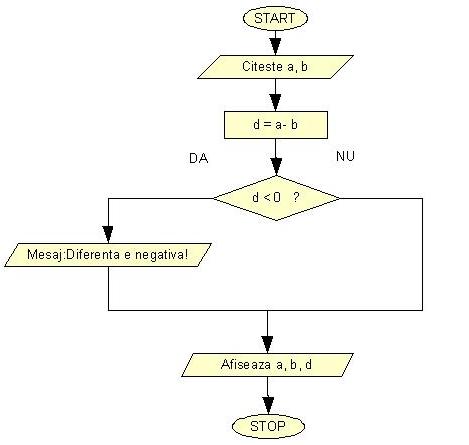
Sa realizam acum schema logica a unui program care asteapata de la utilizator doua numere (a si b) pe care le afiseaza in ordine crescatoare adica in ordinea a,b daca a < b sau b,a daca b < a
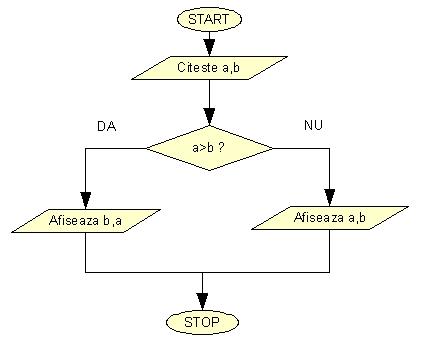
Schema logica a unui program care asteapata de la utilizator coeficientii euatiei de gradul 1 (a si b) si afiseaza solutiile
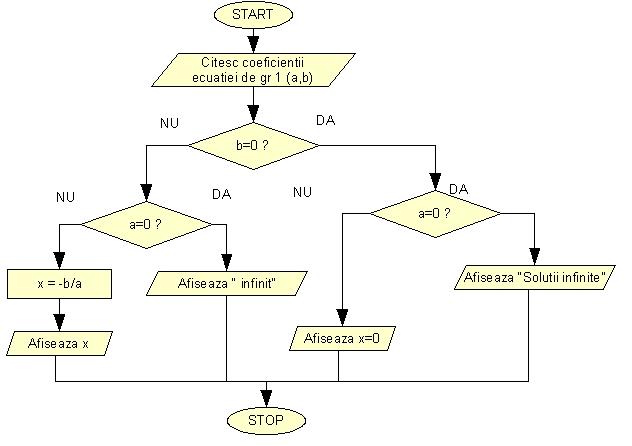
Schema logica a unui program care asteapata de la utilizator coeficientii euatiei de gradul 2 (a, b si c) si afiseaza solutiile
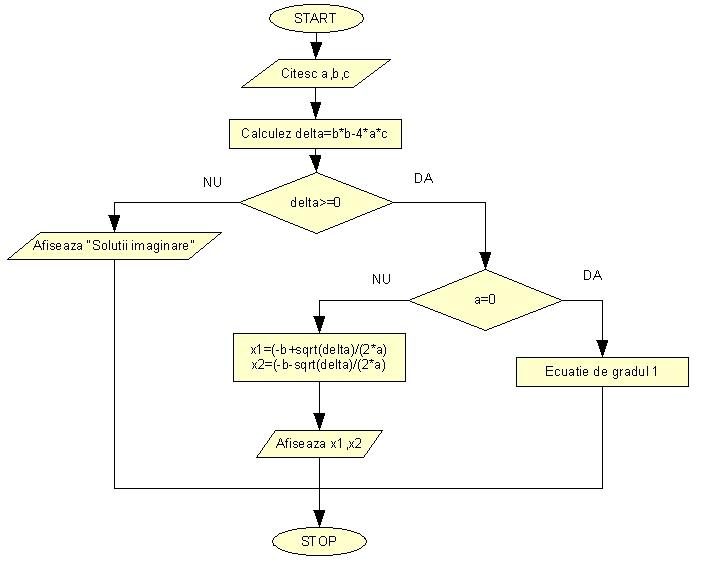
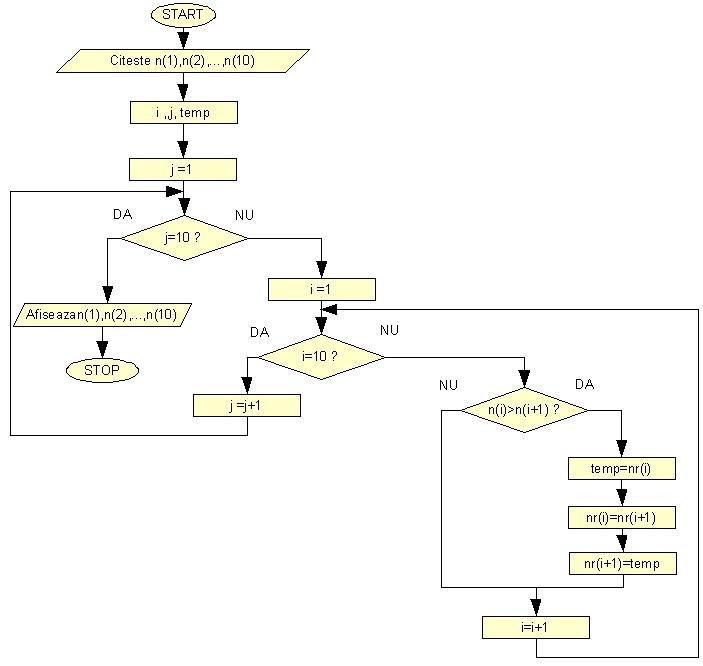
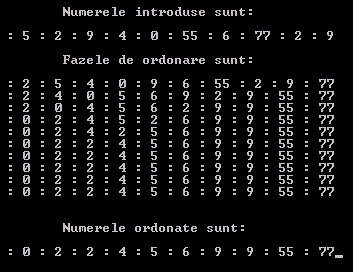
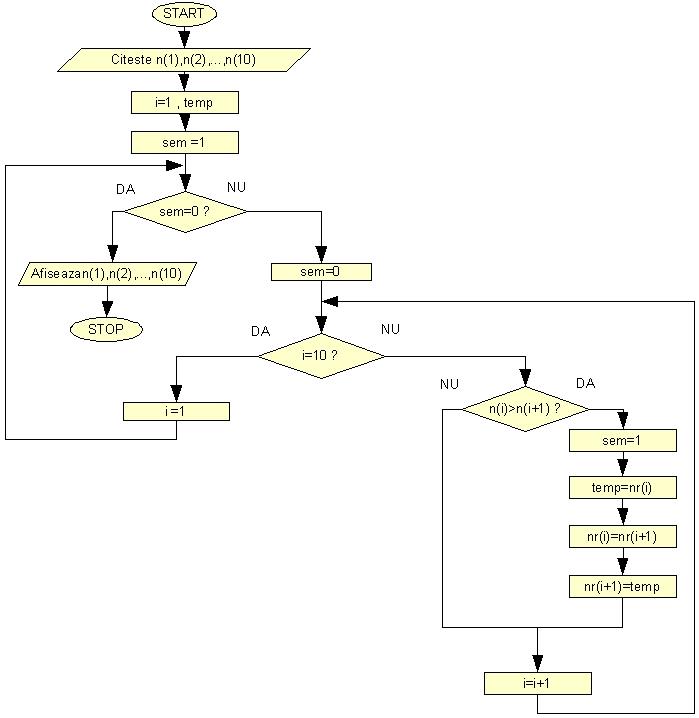
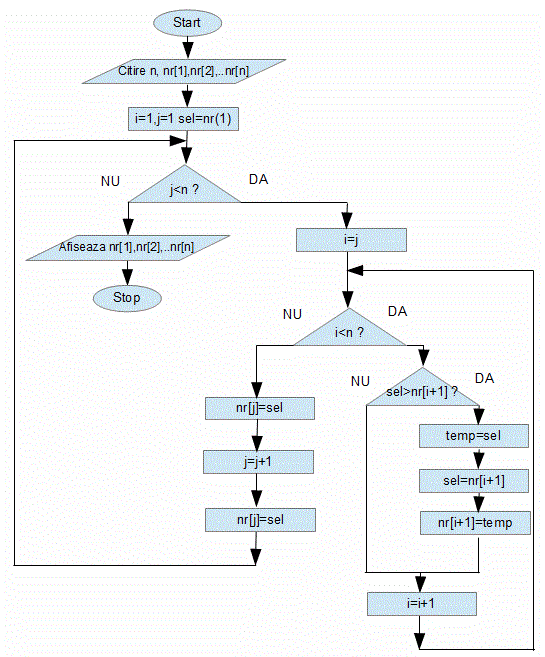
Sa realizam acum schema logica a unui program care asteapata de la utilizator trei numere (a,b si c) pe care le afiseaza in ordine crescatoare.
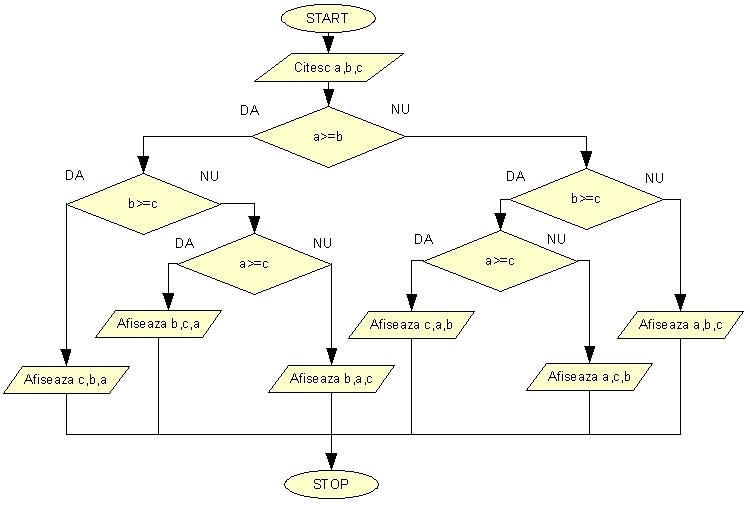
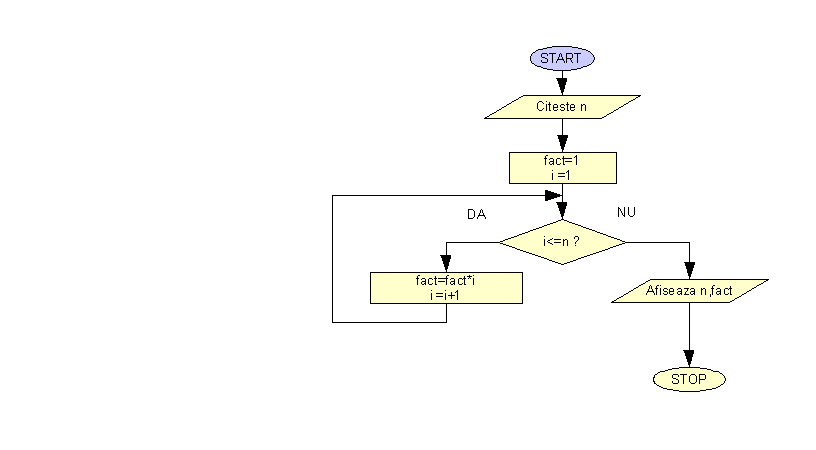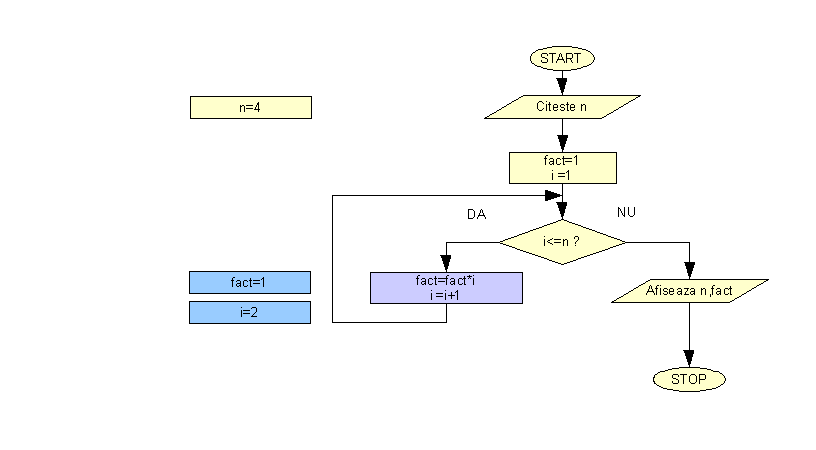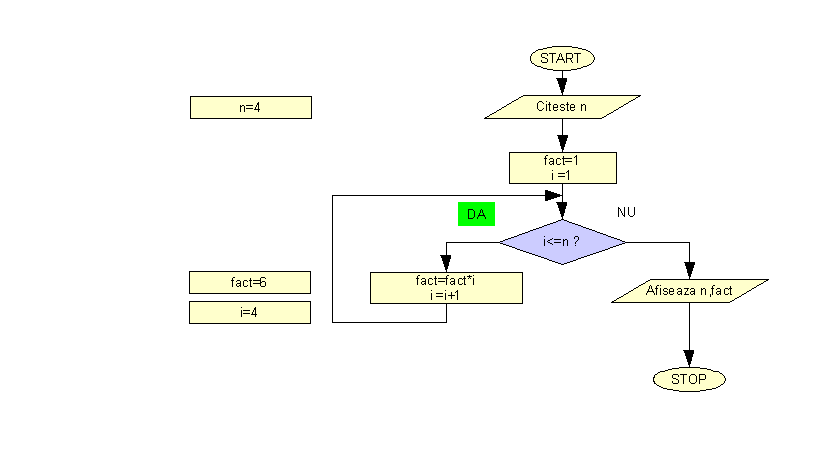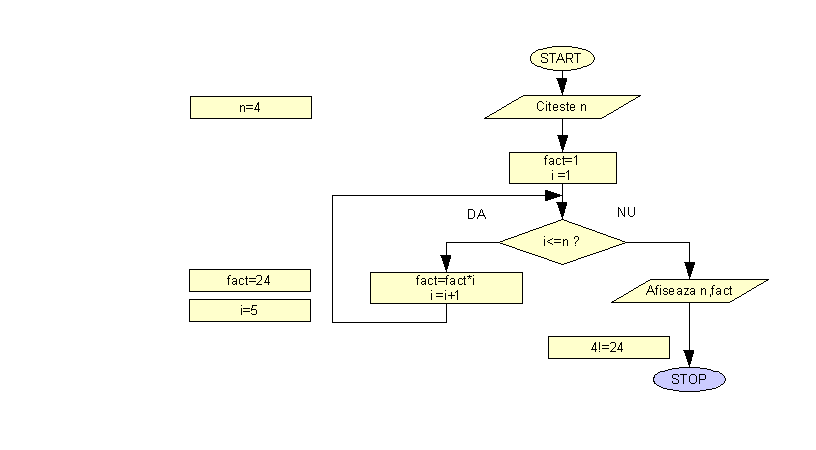
De multe ori e nevoie sa calculam repetitiv ceva. Sa luam de exemplu calculul sumei primelor 100 de numere naturale sau calculul lui n!. Sa realizam schema logica a unui program ce calculeaza n factorial.
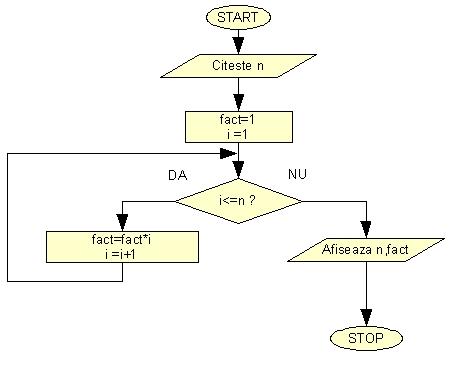
Sa vedem aceasta schema logica afisata animat pentru n=4.
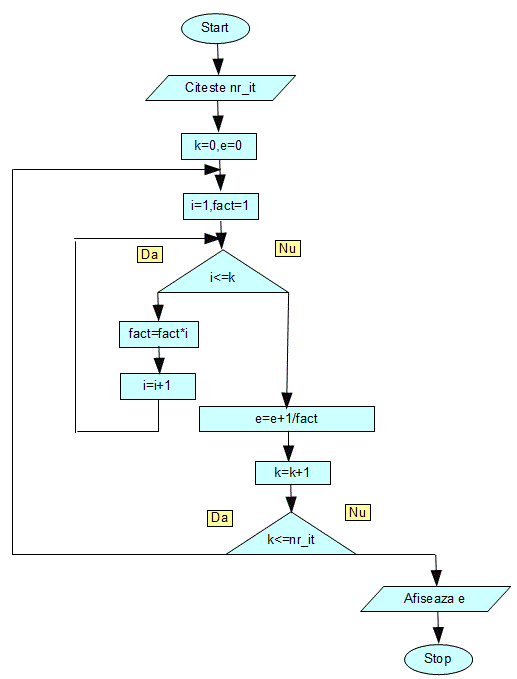
Sa incercam sa calculam cat mai exact valoarea lui e. Numarul e poate fi descompus in serii astfel:
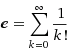
Numarul e va putea fi aproximat prin aplicarea formulei de sus pe un numar finit de pasi astfel:
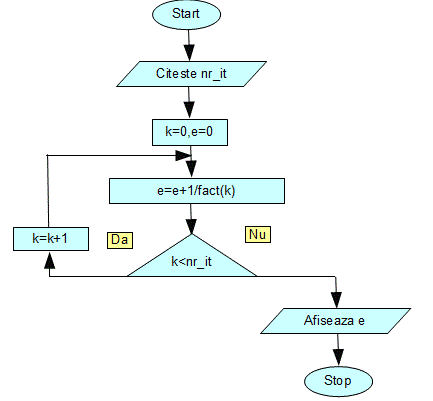
fact(k) fiind aplicatia anterioara pentru calculul factorialului.
Daca includem schema logica a aplicatiei de calcul factorial, schema logica pentru aproximarea numarului e devine: