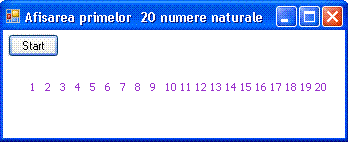
Sa realizam un program care afiseaza primele 10 numere naturale.
// Program scris in C++ Visual Studio 2005 de tipul:CLR console application
// Programul afiseaza primele 10 numere naturale
#include "stdafx.h"
#include < iostream >
using namespace std;
int main(void)
{
int i=1;
cout <<" \n\tNumerele sunt: ";
while (i<=10)
{
cout << i << " ";
i+=1;
}
cin.ignore();
cin.get();
return 0;
}
|
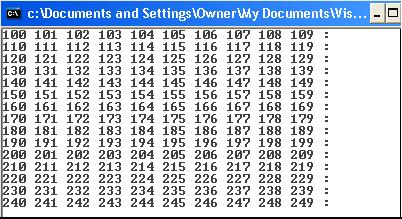
Dupa rularea programului in "Command Prompt" se afiseaza:

Urmatorul program afiseaza 500 numere naturale aleatoare intre 0 si 9.
#include "stdafx.h"
#include < iostream >
using namespace std;
int main(void)
{
int i=0;
while(i < 500)
{
cout << rand()%10 <<" ";
i++;
}
cin.ignore();
cin.get();
return 0;
}
|
Dupa rularea programului in "Command Prompt" se afiseaza:
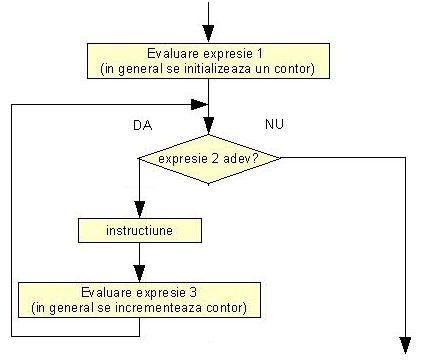
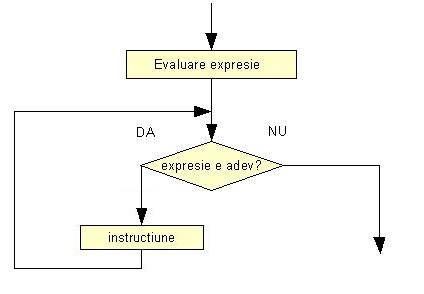
Schema logica de de mai jos, calculeaza n!. Sa realizam programul care implementeaza aceasta schema logica.
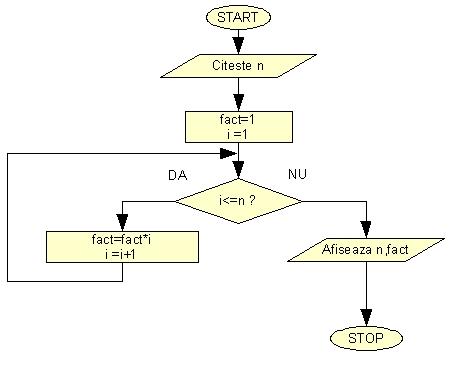
// Programul calculeaza n factorial.
#include "stdafx.h"
#include < iostream >
using namespace std;
int main(void)
{
int i=1,n;
double fact=1;
cout <<" \n\tProgramul calculeaza n Factorial ";
cout <<" \n\n\tIntroduceti numarul n: ";
cin >> n;
while (i<=n)
{
fact*=i;
i+=1;
}
cout <<" \n\n\tRezultat: "<< n << "! =" << fact;
cin.ignore();
cin.get();
return 0;
}
|
Schema logica animata a aplicatiei pentru calculul n! prezinta pas cu pas rularea aplicatiei pentru n=4
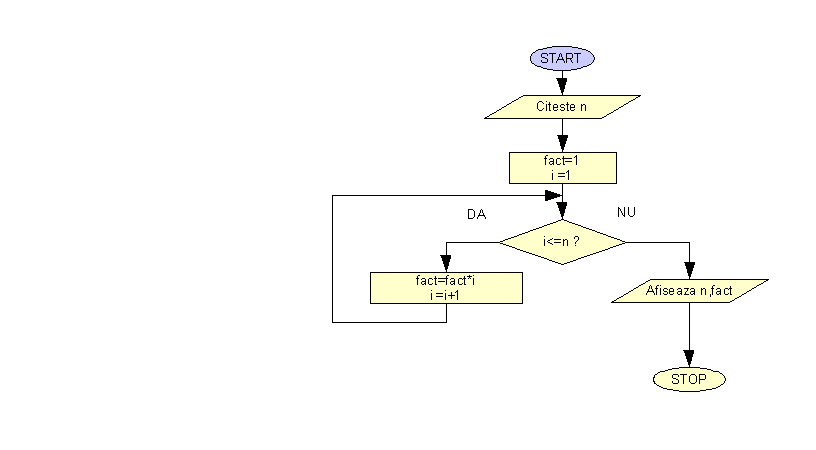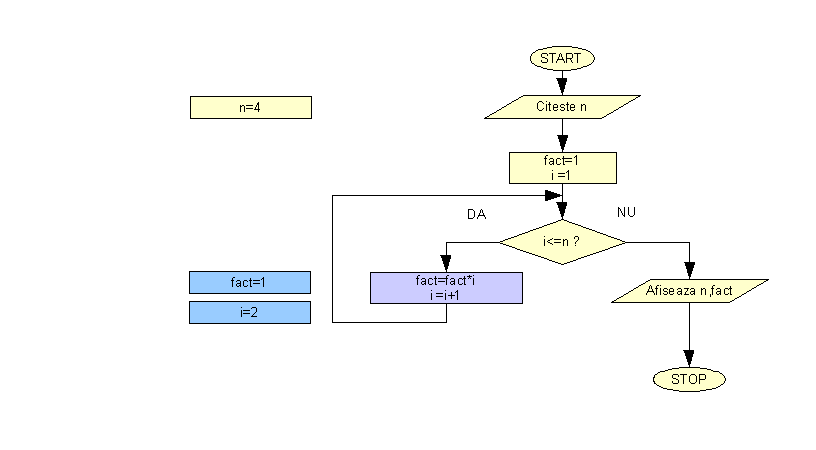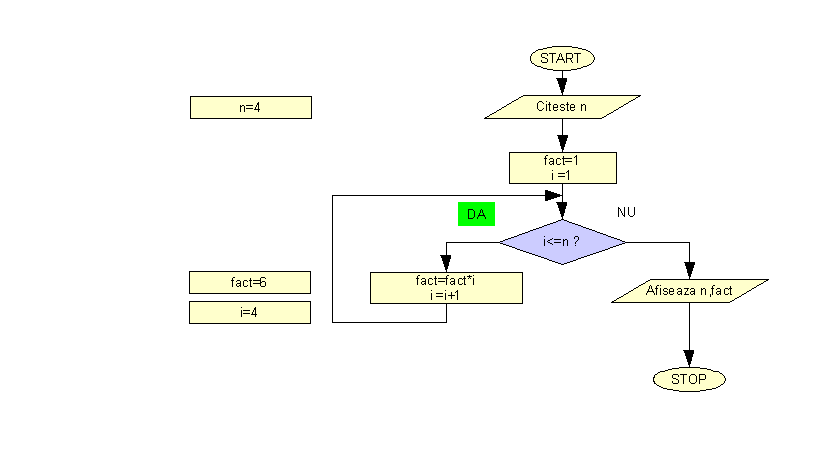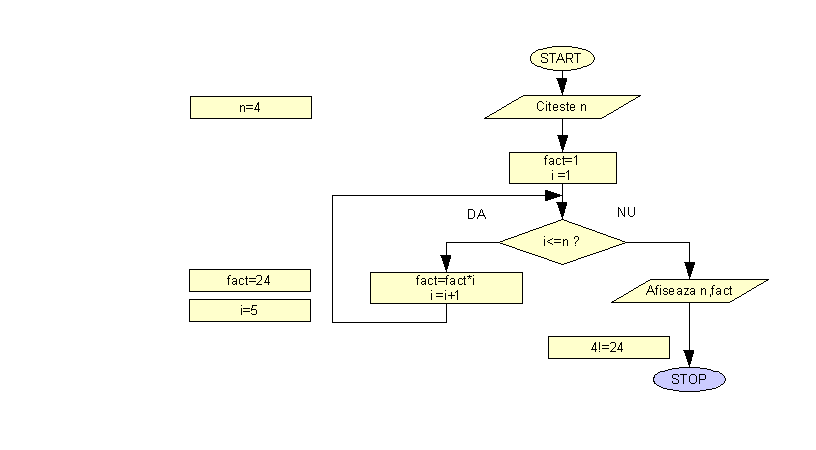
Rularea pas cu pas efectiva a aplicatiei se poate realiza prin plasarea unui Breakpoint in program la inceputul instructiunii repetitive "while".
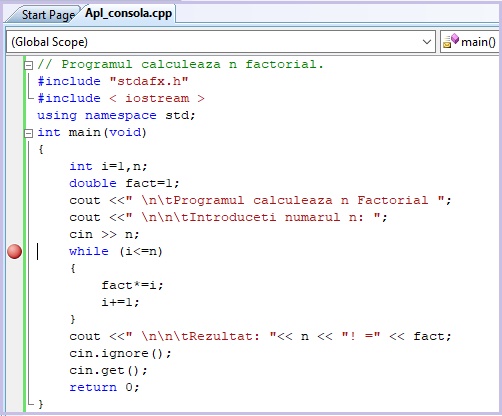
Dupa plasarea Breakpoint-ului programul se lanseaza normal dupa care rularea acestuia se va opri la instructiunea corespunzatoare Breakpoint-ului
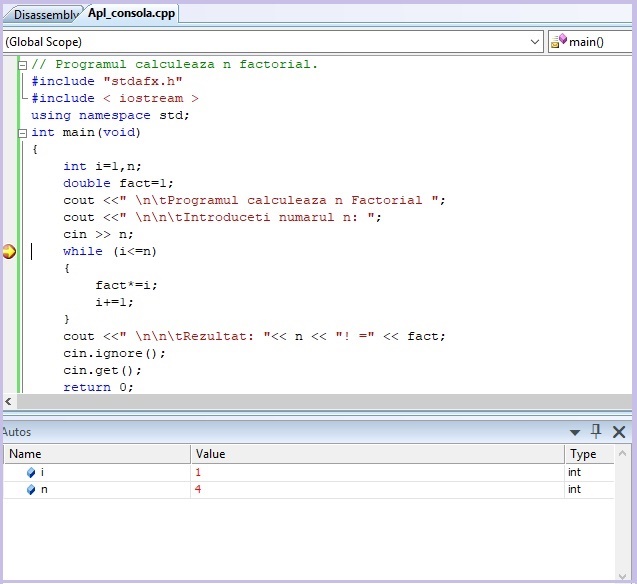
Din acest moment se poate rula pas cu pas prin apasarea tastei F10
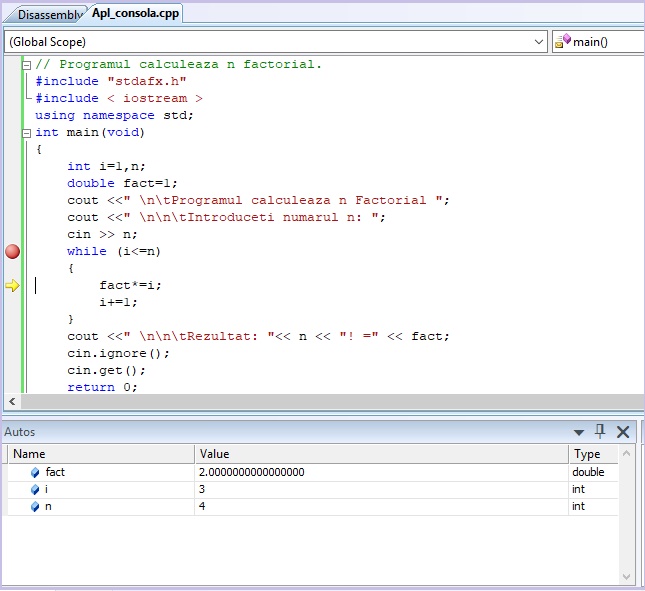
Instructiunile repetitive se pot utiliza pentru calculul integralelor functiilor pe diverse intervale.
Tinand cont ca integrala reprezinta aria suprafetei delimitata de functie pe intervalul dat, aceasta arie se poate calcula prin insumarea ariei dreptunghiurilor cuprinse sub graficul functiei pe intervalul dat. Spre exemplu integrala functiei x2 pe intervalul x0 - x1 este reprezenta in imaginea de jos.
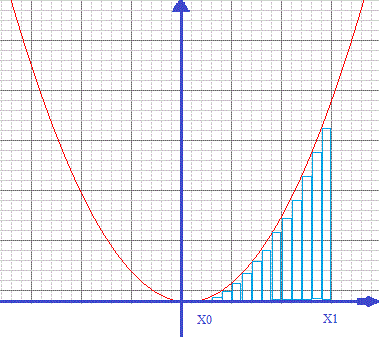
Cu cat impartim intervalul in mai multe dreptunghiuri, calculul integralei se face cu precizie mai mare.
Se poate realiza deci o aplicatie pentru calculul integralei functiei f(x)=x2 pe intervalul x0-x1 astfel:
// Programul calculeaza integrala functiei x^2 pe intervalul 0-10
#include "stdafx.h"
#include < iostream >
using namespace std;
int main(void)
{
double s=0;
double x0=0;
double x1=10;
double nr_pasi=1000000;
const double pas=(x1-x0)/nr_pasi;
double x=x0;
while (x<=x1)
{
s=s+x*x*pas;
x=x+pas;
}
cout <<" \n\tIntegrala este: " << s;
cin.ignore();
cin.get();
return 0;
}
|
Primitiva functiei x2 este x3/3. Pe intervalul [0-10] integrala este 1000/3=333.333
Daca se ruleaza programul cu nr_pasi=1000 obtinem rezultatul 333.834
Daca se ruleaza programul cu nr_pasi=10000 obtinem rezultatul 333.383
Daca se ruleaza programul cu nr_pasi=100000 obtinem rezultatul 333.338
Daca se ruleaza programul cu nr_pasi=1000000 obtinem rezultatul 333.334
Daca se ruleaza programul cu nr_pasi=10000000 obtinem rezultatul 333.333
Se observa ca eroarea depinde de finetea pasului (numarul de pasi).
Instructiunea while se foloseste la fel si in modul grafic Windows Forms Application. Sa folosim instructiunea while pentru a afisa o serie de dreptunghiuri concentrice de forma celor de mai jos:

n_dreptunghiuri
Deschidem un nou proiect Windows Forms Application intitulat "n_dreptunghiuri". De aceasta data nu mai plasam nici un Buton. Vom pune procedura noastra sa se execute odata cu deschiderea aplicatiei.
Completam procedura deschisa pe evenimentul paint al form-ului cu:
C#
int i,j,h,w,d,n=10;
// i contor dreptunghiuri concentrice
// n nr dreptunghiuri concentrice
System.Drawing.Graphics Desen;
Desen = this.CreateGraphics();
System.Drawing.Pen Creion_albastru;
Creion_albastru =new System.Drawing.Pen(System.Drawing.Color.Blue);
Desen.Clear(this.BackColor);
h=this.Height-30; //inaltimea maxima a dreptunghiurilor
w=this.Width; //latimea maxima a dreptunghiului
d=h/2/n; //distanta intre doua dreptunghiuri concentrice
i=0;
while (i<=d*n){
Desen.DrawRectangle(Creion_albastru, i+10, i+10, (w-30-2*i), (h-30-2*i));
i+=d;
}
|
Se observa ca inainte de trasarea dreptunghiurilor s-a sters ecranul cu instructiunea:
Desen.Clear(this.BackColor);
Instructiunea: Desen.DrawRectangle(Creion_albastru, i+10, i+10, (w-30-2*i), (h-30-2*i)); traseaza un dreptunghi incepand cu pozitia x1=i la care s-a adaugat o margine de 10 pixeli si y1=i la care s-a adaugat o margine de 10 pixeli. Latimea dreptunghiului este w latimea maxima calculata - 2 margini de 15 pixeli adica 30 -2*i adica. I se incrementeaza cu d, d fiind distanta calculata intre doua dreptunghiuri Inaltimea este h -30-2*i similar cu latimea dreptunghiului.
In cadrul instructiunii while se pot insera si alte instructiuni de exemplu instructiunea if .
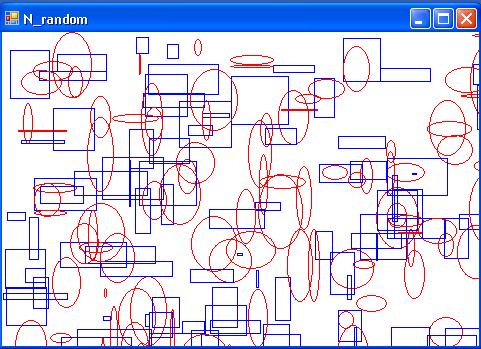
Vom folosi in continuare instructiunea if in cadrul instructiunii while in modul grafic Windows Forms Application pentru a desena mai multe dreptunghiuri de dimensiuni aleatoare pentru a imita blocurile turn din centrul unui oras.
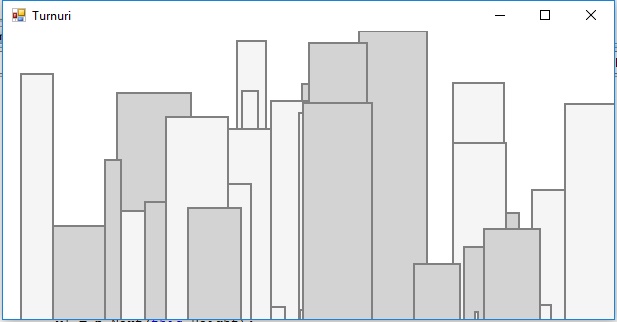
turnuri
Deschidem un nou proiect C# Windows Forms Application intitulat "turnuri". Vom pune procedura pentru desenarea turnurilor sa se execute odata cu deschiderea aplicatiei si anume pe evenimentul "paint".
Pentru a obtine valori aleatoare, vom crea un obiect n prin instantierea clasei "System.Random" si vom invoca metoda "Next".
Completam procedura deschisa pe evenimentul paint al form-ului cu:
C#
int i, x1, y1, w, h;
System.Drawing.Graphics Desen;
System.Drawing.SolidBrush Pens_g, Pens_w;
System.Drawing.Pen Creion_g;
Desen = this.CreateGraphics();
Pens_g = new System.Drawing.SolidBrush(System.Drawing.Color.LightGray);
Pens_w = new System.Drawing.SolidBrush(System.Drawing.Color.WhiteSmoke);
Creion_g = new System.Drawing.Pen(System.Drawing.Color.Gray, 3);
System.Random n = new System.Random();
Desen.Clear(this.BackColor);
i = 0;
while (i <= 50)
{
x1 = n.Next(this.Width);
y1 = n.Next(this.Height);
w = n.Next(75);
h = this.Height - y1;
if (i % 2 == 0)
{
Desen.DrawRectangle(Creion_g, x1, y1, w, h);
Desen.FillRectangle(Pens_g, x1 + 1, y1 + 1, w - 1, h - 1);
}
else
{
Desen.DrawRectangle(Creion_g, x1, y1, w, h);
Desen.FillRectangle(Pens_w, x1 + 1, y1 + 1, w - 1, h - 1);
}
i++;
}
|
Ingineria electrica se ocupa in general de studiul si utilizarea semnalelor electice de diferite forme, valori si intensitati. Un mare rol important il are analiza semnalelor electrice, analiza care presupune in primul rand vizualizarea acestora. Exista o serie de dispozitive menite sa afiseze formele de unda a diferitelor semnale electrice (osciloscoape, vobuloscoape, analizoare spectrale etc..). De multe ori aceste semnale pot fi modelate matematic si simulate pe calculator. Vom incerca in continuare sa folosim programarea in mod grafic pentru a afisa diverse forme de unda ale diferitelor semnale electrice. Vom incepe prin a genera un grid peste care urmeaza in viitor sa trasam formele de unda.
Sa incercam sa realizam aplicatia care traseaza urmatorul grid pe ecran:

grid
Deschidem un nou proiect Windows Forms Application intitulat "grid". Nu inseram nici un obiect pe form.
Completam procedura deschisa pe evenimentul paint al form-ului cu:
C#
int i=0;
System.Drawing.Graphics Desen;
Desen = this.CreateGraphics();
System.Drawing.Pen Creion_gri;
Creion_gri=new System.Drawing.Pen(System.Drawing.Color.LightGray);
Desen.Clear(this.BackColor);
// linii verticale
while (i<=this.Width){
Desen.DrawLine(Creion_gri, i, 0, i,this.Height);
i+=10;
}
// linii orizontale
i=0;
while (i<=this.Height){
Desen.DrawLine(Creion_gri, 0, i,this.Width,i);
i+=10;
}
|
Se observa ca inainte de trasarea liniilor orizontale si verticale s-a sters ecranul cu instructiunea:
Desen.Clear(this.BackColor);
Daca dorim sa accentuam unele linii adica sa realizam un grid mai mare peste gridul mic sa zicem tot la 5 griduri mici sa trasam cate un grid mai mare procedam astfel: daca ne aflam pe pozitia 10*5=50 schimbam culoarea cu un gri mai intens si optinem imaginea:
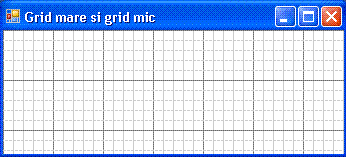
grid_mm
C#
int i=0;
System.Drawing.Graphics Desen;
Desen = this.CreateGraphics();
System.Drawing.Pen Creion_gri_d;
Creion_gri_d=new System.Drawing.Pen(System.Drawing.Color.LightGray);
System.Drawing.Pen Creion_gri;
Creion_gri=new System.Drawing.Pen(System.Drawing.Color.Gray);
Desen.Clear(this.BackColor);
// linii verticale
while (i<=this.Width){
if (i%50==0)
Desen.DrawLine(Creion_gri, i, 0, i,this.Height);
else
Desen.DrawLine(Creion_gri_d, i, 0, i,this.Height);
i+=10;
}
// linii orizontale
i=0;
while (i<=this.Height){
if (i%50==0)
Desen.DrawLine(Creion_gri, 0, i,this.Width,i);
else
Desen.DrawLine(Creion_gri_d, 0, i,this.Width,i);
i+=10;
}
|
Se observa ca s-a folosit functia % numita si functia mod functie care ne returneaza restul impartirii. In cazul de fata am testat daca restul impartirii lui i cu 50 este 0 si atunci am schimbat culoare de la gri_d la gri.
Instructiuni while imbricate:
Instructiunile while se pot insera unele in altele pe oricate nivele. Se spune ca s-a imbricat o instructiune while in alta instructiune while. Sa reluam aplicatia de desenare a n dreptunghiuri concentrice si sa desenam m grupuri de cite n dreptunghiuri concentrice. Vezi imaginea de jos.:

n_x_m_dreptunghiuri
Singura diferenta se gaseste in procedura atasata evenimentului pain al form-ului care devine:
C#
int i,j,h,w,d,m=3,n=10;
// j contor dreptunghiuri
// i contor dreptunghiuri concentrice
// m nr dreptunghiuri
// n nr dreptunghiuri concentrice
System.Drawing.Graphics Desen;
Desen = this.CreateGraphics();
System.Drawing.Pen Creion_albastru;
Creion_albastru =new System.Drawing.Pen(System.Drawing.Color.Blue);
Desen.Clear(this.BackColor);
h=this.Height-30; //inaltimea maxima a dreptunghiurilor
w=this.Width/m; //latimea maxima a dreptunghiului
d=w/2/n; // distanta intre doua dreptunghiuri concentrice
j=0;
while (j<=m*w){
i=0;
while (i<=d*n){
Desen.DrawRectangle(Creion_albastru, j+i+10, i+10, (w-20-2*i), (h-20-2*i));
i+=d;
}
j+=w;
}
|
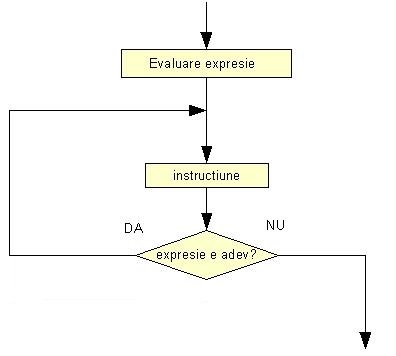
Instructiunea do while :
Instructiunea do while Se foloseste pentru a executa repetitiv o instructiune sau o secventa de instructiuni atata timp cat o expresie este adevarata, insa testul are loc dupa executia instructiunii deci ea se va executa cel putin o data.